R package oneinfl
The R package oneinfl estimates one-inflated positive Poisson (OIPP) and one-inflated zero-truncated (OIZTNB) regression models. When count data are truncated so that $y = 1,2,\dots$, it is also often inflated at $y=1$. The current standard model for treating such data is the zero-truncated negative binomial (ZTNB) model. ZTNB fails to account for excess 1s (or too few 1s), resulting in biased and inconsistent estimators.
This vignette illustrates oneinfl by reproducing and extending the MedPar results in “One-inflated zero-truncated count regression models” (Godwin, 2023). Please cite this paper when using oneinfl.
Load package and data
Load the oneinfl package using:
devtools::install_github("rtgodwin/oneinfl")
library(oneinfl)
Load the medpar data from the msme package:
library(msme)
data(medpar)
data = medpar
oneinfl(formula, data, dist): estimate OIZTNB and OIPP
Estimate the one-inflated zero-truncated negative binomial (OIZTNB) model:
formula <- los ~ white + died + type2 + type3 | white + died + type2 + type3
OIZTNB <- oneinfl(formula, data, dist="negbin")
OIPP <- oneinfl(formula, data, dist="Poisson")
formula is the population model to be estimated, variables that precede | link to the mean function and variables that follow | link to one-inflation. data is a data frame and dist="negbin" estimates OIZTNB while dist="Poisson" estimates OIPP.
truncreg(formula, data, dist): estimate ZTNB and PP models
These are the current standard models for treating zero-truncated count data. Estimate them in oneinfl using:
formula <- los ~ white + died + type2 + type3
ZTNB <- truncreg(formula, data, dist="negbin")
PP <- truncreg(formula, data, dist="Poisson")
oneLRT(model1, model2): test for overdispersion and one-inflation
oneLRT extracts the log-likelihood and number of parameters in any two models estimated by oneinfl or truncreg. It returns the likelihood ratio test statistic and its associated p-value. It can be used to test hypotheses involving nested models.
Overdispersion
Likelihood ratio test for overdispersion:
oneLRT(OIZTNB, OIPP)
$LRTstat
[1] 3305.341
$pval
[1] 0
We reject the null hypothesis of no overdispersion. Overdispersion is a well-developed topic that has led many to discard a Poisson model in favour of a negative binomial model. The principle extends to both truncated data (the ZTNB model vs. the PP model) and one-inflation (OIZTNB vs. OIPP).
One-inflation
Likelihood ratio test for one-inflation:
oneLRT(OIZTNB, ZTNB)
$LRTstat
[1] 131.4165
$pval
[1] 0
The LRT supports the presence of one-inflation (the null hypothesis is no one-inflation).
oneWald(oneinfl.model): test for one-inflation
Godwin (2023) presents a Wald test for the presence of one-inflation. Only the one-inflated models need be estimated; oneinfl.model should be a OIZTNB or OIPP model estimated by oneinfl.
oneWald(OIZTNB)
$W
[1] 469.1062
$pval
[1] 0
The Wald test also supports the presence of one-inflation.
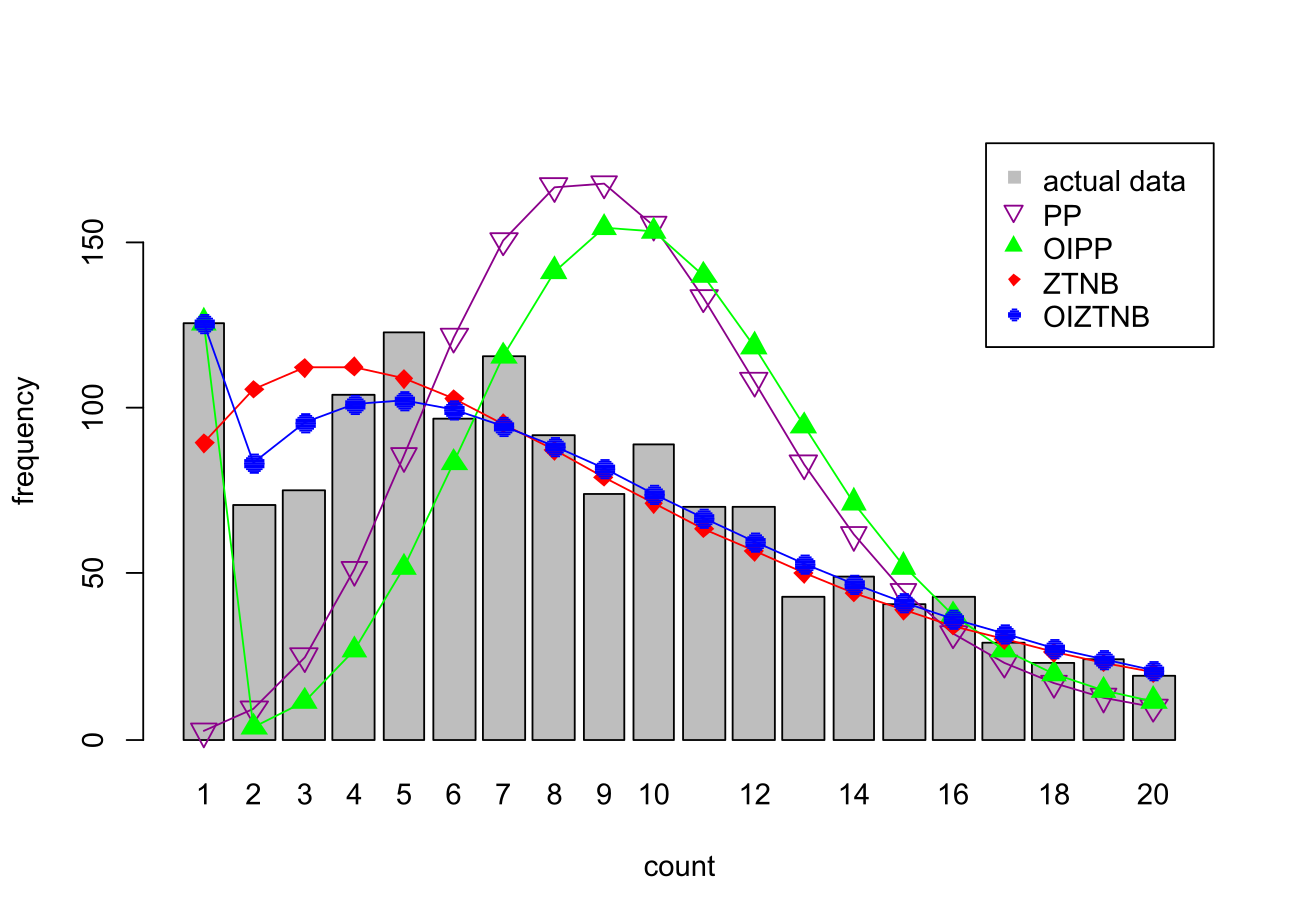
oneplot(model1, model2, model3, model4): plot actual and predicted counts
In Godwin (2023) only the OIZTNB and ZTNB models are plotted, but here we plot all of the estimated models using:
oneplot(PP, OIPP, ZTNB, OIZTNB, data=data, maxpred=20, ylimit=180)
which produces the following plot:
summary.oneinfl(model): summarize
summary.oneinfl(model) is a custom summary function for OIZTNB, OIPP, ZTNB, and PP models estimated using oneinfl, which provides output similar to standard uses of summary(). For the OIZTNB model:
summary.oneinfl(OIZTNB)
Call:
formula: los ~ white + died + type2 + type3 | white + died + type2 + type3
distribution: negbin
Coefficients (beta):
Estimate Std.Error z_value p.value
b(Intercept) 2.29913 0.07184 32.005 0.000e+00 ***
bwhite -0.09708 0.07138 -1.360 1.738e-01
bdied -0.06814 0.04492 -1.517 1.293e-01
btype2 0.23413 0.05349 4.377 1.204e-05 ***
btype3 0.75580 0.07884 9.586 0.000e+00 ***
Coefficients (gamma):
Estimate Std.Error z_value p.value
g(Intercept) -4.2002 0.5060 -8.300 0.00000 ***
gwhite 0.6594 0.4814 1.370 0.17075
gdied 2.3349 0.2359 9.899 0.00000 ***
gtype2 -0.5413 0.2829 -1.913 0.05569 .
gtype3 -0.7507 0.4472 -1.679 0.09324 .
alpha:
Estimate Std.Error z_value p.value
1 2.267 0.146 15.53 0 ***
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
average one-inflation: 0.0416855179433309
average absolute one-inflation: 0.0680909723883016
Log-likelihood: -4671.06423844655
For example, when the variable $died = 1$, one-inflation increases significantly, but $died$ otherwise does not effect los. Average one-inflation is 4.2% (there is an additional 0.042 probability that each person will stay only 1 day). Average absolute one-inflation is 0.068, meaning that some observations have one-deflation (e.g. when $type2$ or $type3$ equals 1).
To reproduce the results form Chapter 11.1 in Hilbe (2011), we summarize the ZTNB model using:
summary.oneinfl(ZTNB)
Call:
formula: los ~ white + died + type2 + type3
distribution: negbin
Coefficients (beta):
Estimate Std.Error z_value p.value
b(Intercept) 2.3334 0.07499 31.115 0.000e+00 ***
bwhite -0.1318 0.07469 -1.765 7.755e-02 .
bdied -0.2512 0.04468 -5.622 1.889e-08 ***
btype2 0.2601 0.05529 4.704 2.550e-06 ***
btype3 0.7692 0.08259 9.314 0.000e+00 ***
alpha:
Estimate Std.Error z_value p.value
1 1.881 0.1034 18.19 0 ***
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Log-likelihood: -4736.77246562658
Taking exp(ZTNB$beta) gives the incident risk ratios.
signifWald(model, "var.name"): tests of significance
Since variables are typically linked to both the rate parameter $\lambda$ and the one-inflating parameter $\omega$, tests of overall significance are joint hypotheses. Testing the overall significance of the variable $white$ for example, we can use:
signifWald(OIZTNB, "white")
$W
[1] 3.725885
$pval
[1] 0.1552153
The p-value of 0.155 suggests that the variable does not have a significant effect on $los$, which is contrary to the standard ZTNB model.
margins(model, data): estimate marginal effects and their standard errors
Marginal effects can be estimated at the default “average effects” (the marginal effect is estimated at each observation and averaged over all observations):
margins(OIZTNB, data)
Call:
formula: los ~ white + died + type2 + type3 | white + died + type2 + type3
distribution: negbin
Marginal effects:
Marginal.effects Std.Error z_value p.value
white -1.258 0.7344 -1.713 8.668e-02 .
died -2.189 0.3964 -5.522 3.343e-08 ***
type2 2.575 0.5875 4.382 1.174e-05 ***
type3 10.142 1.4663 6.917 4.616e-12 ***
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
these marginal effects can be compared to other models estimated by oneinfl, for example using:
margins(ZTNB, data)
Marginal effects can be estimated at the “effect at means” (the data is averaged before evaluating the marginal effect):
margins(OIZTNB, data, at = "EM")
or at a representative case:
margins(OIZTNB, data, at = list(white = 0, died = 0, type2 = 0, type3 = 0))
pred(model, data): predicted values
Generate predicted counts from an OIZTNB model:
pred(OIZTNB, data)
or from any of the four models:
pred(ZTNB, data)
Random variate generation
Random variates can be generated using roipp(b, g, X, Z) and roiztnb(b, g, a, X, Z). For example:
n <- 100
X <- data.frame(rep(1, n), rnorm(n))
Z <- X
roipp(b=c(0, 0), g=c(0, 0), X, Z)
roiztnb(b=c(0, 0), g=c(0, 0), a=1, X, Z)
Generate the expected response
| To evaluate $E[y_i | \hat{\theta_i}]$ use: |
predict.oneinfl(model = OIZTNB, data = medpar)
for example.